Ed Byars: We have all been looking forward to this next one. A lot of things have been said about McCready speeds, Dolphin flying and all kinds of good things like that. Wil has actually made a quantitative analysis of this and now he is going to tell us the price we pay for not flying McCready speeds -- maybe it is a high price, maybe it is a low price; I can't wait to hear. Wil Schuemann.
Wil Schuemann: Since Paul McCready worked out his little computer a ways back a lot has been said about it. The part I'm interested in is not so much the specific figures or curves or in trying to convince you what to do in any particular glider, but in trying to give you a general flavor. The calculations that go into the kind of curves that I am generating are fairly simple but very laborious if you don't happen to have a computer around. They are also the kind of things you can do without equations by just thinking it through in your head. A second thing is that there are a lot of options with regard to McCready speeds. There are a lot of different ways to manage this sort of thing. I think it is going to come through that I don't believe in it very much before we are all done. I have done a lot of calculations in a theoretical way to justify this belief. The calculations were done after I had made up my mind what was the best way to fly. I think you will find that most of the best pilots tend to fly this way anyway. The curves are about a fixed glider and a fixed condition. I am not the least bit interested in the details of the thermal, but will talk about curves, you are really doing a parametric analysis. All parametric analysis means is that you consider a number of things that are related, such as the glider polar, the thermal strength and the inter-thermal sink. The thermal strength is the motion of the air in the thermal -- not the climb rate of the glider. The inter-thermal sink is the motion of the air between thermals, not the vertical motion of the glider. The inter-thermal speed is the speed you fly your glider. The average speed is the speed achieved over any length that you fly, including the time it takes to climb back to altitude. All of these are related to a theoretical sense by equations. If you want to display the results, you have to set some of them equal to constants and let others vary. Then you can plot things on graphs.

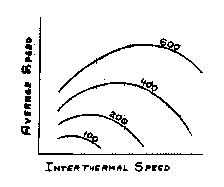
Figure 1 is the kind of curve Dick Johnson presented yesterday. It is by far the most familiar kind. You hold sink and the sailplane polar constant and then plot the average speed achieved for a course against the inter-thermal speed. This is the speed to fly and for different thermal strengths you can find the relationship. If for instance you are achieving 100 ft./per minute climb in thermals you pick the point at the top of the 100 ft. curve, and below it you read the inter-thermal speed to fly. If you are achieving 200 ft./per minute you read the 200 ft. curve the same way, etc. I am sure you are all familiar with this type of curve.
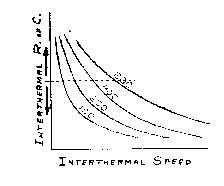
Figure 2 is a graph that usually isn't shown but is the basis from which the McCready speed ring is built. You plot the sink or climb, or the rising and falling of air between thermals on one axis, and your inter-thermal speed on the other. The curves are for different amounts of lift. You can see that if you pick values from this curve you can plot what your inter-thermal speed should be as a function of the rising and falling of the air between thermals. That's where McCready speed curves come from.
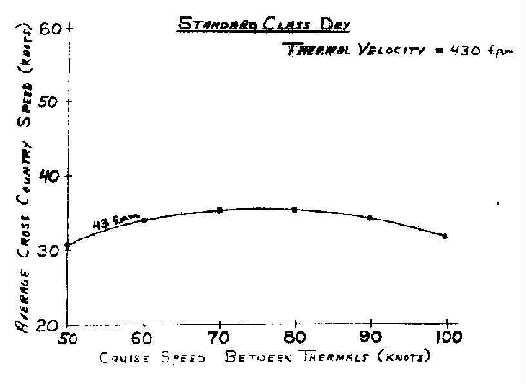
I am not going to talk about either of these curves. Rather I am going to do something a little different. In Figure 3 the thermal velocity is fixed. It's 430 feet per minute. This means that in a standard class ship without water you are going to be achieving roughly 300 feet per minute R/C, this is a typical eastern U.S. condition. In Figure 3 as in Dick Johnson's curve, the average cross country speed in knots is plotted against the cruise speed between the thermals. I have drawn a curve for a specific rate of sink of air between the thermals. If you are flying through average sink of 43 feet per minute (that's air motion) then clearly the optimum speed to fly is 75 knots. But you don't lose much by flying 70 and you don't lose much by flying 80. You can fly 65 and hardly argue about the difference, so it is a very broad function. And so there must be other reasons for choosing the exact speed to fly. Suppose you want to choose whether to fly 65 or 75. In one case, obviously you are going to make a little more speed. But suppose you want to drop back to 65, are you going to actually have more range or are you going to have less range? Because you are going to fly slower in sink are you really sure whether you are going to have more range or less range? If you are going to have more range, it is clearly to your benefit to slow up depending upon future conditions, of course.
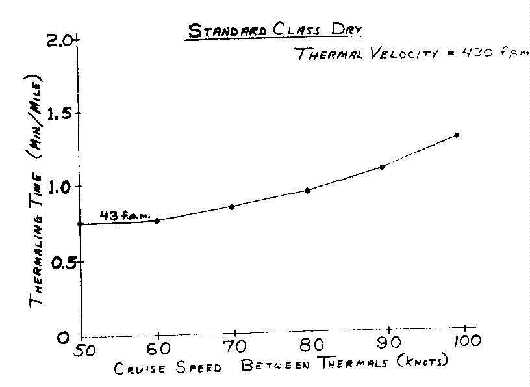
In answer to this question we go to Figure 4. The thing on the border is a kind of a cute unit but very useful. Thermalling time in minutes per mile is very interesting because it takes into account a ship that's dry or wet or open or whatever. It gives you a real idea of how many minutes a ship is going to have to thermal to finish a cross country task. It's really a measure of how much risk you are taking on a cross country flight. The more thermal minutes in a given flight means the more thermals you have to find. Minimizing thermalling time in minutes per mile is the name of the game. The horizontal axis is your cruise speed. I have plotted the same amount of sink as in Figure 3 so you can see the faster you fly the more miles per minute it takes in thermalling time to regain your altitude. We said the optimum speed was 75 knots. This turns out to be .9 minutes per mile thermalling time. If you slow up to 65 you are achieving essentially the same speed but you're down to .8 minutes per mile. You lose a small fraction in speed but in terms of your thermalling requirements you save 12%. That, for my way of flying, is a good bargain.
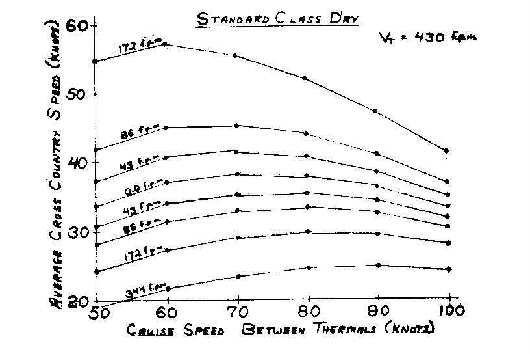
Now I have expanded on these curves so don't get overwhelmed by Figure 5. It is the same curve presented before, it shows your average cross country speed against your cruise speeds between thermals. Only this time I have shown it as a function of different rates of climb and rates of sink between thermals. ( A ) is the curve we had before at 43 feet per minute and the optimum speed to fly is about 75 knots. I'm arguing that maybe a speed of 65 is a pretty good choice. If you are flying through still air, (B) is 0.0 feet per minute. Your optimum speed drops to about 70 and you can probably do well at around 60 to 65. If you continue to fly into lift, 86 feet per minute (C) is coming up on zero sink on your variometer.
If you can get 172 feet per minute (D) which is essentially half of the thermal strength, you can slow up to 60 knots and achieve an average cross country speed of 57 knots when you are only flying 60 knots -- that's very nice. Going the other way, you get into a sink al; 86 (E) and 172 (F) feet per minute, the curve starts to shift to the right. If you have 172 feet per minute sink you have to add 172 to your glider polar and that looks pretty grim, over 300 feet per minute total sink. The optimum speed moves up to 80 knots or more but still you have latitude to play with. The question now becomes more interesting at 344 feet per minute down, you have to go to 90 knots to get the optimum cross country speed. Now, you say, "I am going to slow up to 80 or to 76 and sacrifice some of my achieved speed in order to increase my range." In that kind of sink I am not sure you increase your range. If you fly the McCready curve for this condition and you get into real heavy sink, it will lead you up to 90 knots and some people argue that that's the way to fly. But what Dick Johnson was arguing for yesterday was to shift down to some percent of that speed and fly a new curve. There is a third alternative. Let's suppose for this same condition that you are flying along as you fly most of the time when you are not in a panic but just trying to achieve the best flight you can for the day. I am going to argue that flying 75 knots almost all the time is a pretty good choice. If you fly through essentially still air in moderate sink at 75 knots you are going to achieve about the best speed that you can. When you fly into sink you will not lose very much in the way of achieved cross country speed. Seventy-five knots is just not very much different from optimum -- a fraction of a mile per hour in achieved cross country speed. If you have a moderate amount of lift between thermals, 75 knots still is not a bad choice. If you get some real lift, that's going to show positive, you can just slow up a little bit. I don't believe in slowing up very much. I am offering this alternative, fly 75 knots all the time, unless you hit a thermal, and then slow up to 65 knots.
Question: What ship is this for?
Answer: All the standard class ship curves are identical.
Question: How did you get away with not computing for the wind factor?
Answer: This is assuming still air. If you want to add headwinds and tailwinds you have more graphs and that's getting away from the point I am trying to make. I am trying to use these curves as a means of developing a philosophy. I find they show a trend or an apparent optimum way to do things.
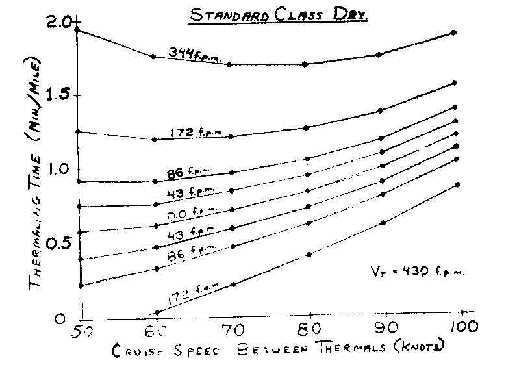
Figure 6 is an expanded curve to answer some of these questions. This shows your thermalling time in minutes per mile against cruise speed. As noted before flying at 65 instead of 75 saves you a lot of thermalling time. As you fly into more sink, your thermalling time increases just as you would expect it to. At 172 feet per minute sink between thermals you begin to pay a penalty for flying too slow. It is interesting to notice that when you get into heavy sink there is a minimum in the required number of thermal minutes per mile at about 75 knots. This means you are going to maximize your range if you fly 75 knots in heavy sink. That's quite contradictory to the McCready curve. Most people push it up to 90 knots when they get into heavy sink. They are actually getting into the part of the curve where they are losing a little range and are decreasing their time in the air by 25 to 30%. Then they haven't got that extra time to think. One of the observations that comes out of this is that when you get into heavy sink fly at 75 knots and start thinking. You have more time to do it. You are going to go farther and have more options. 75 knots is true of all sailplanes under all conditions. It is just something that comes about because the polar curves [go] down so quickly in that speed range. 75 knots is your maximum range speed any time in heavy sink. On the other end of the spectrum when you start to get lift between thermals the thermal requirements naturally go down. If you can maintain a level of lift calling for a speed of 58 knots you can complete the whole course without circling.
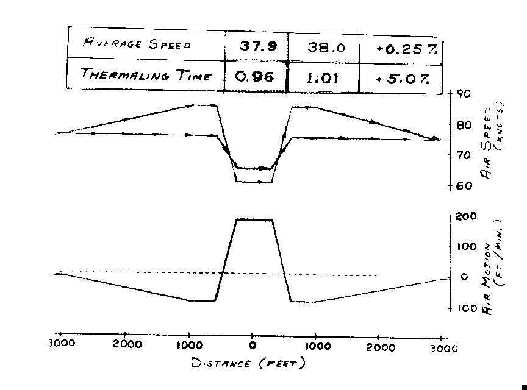
We still haven't really answered the question: "How much do you gain by flying McCready as opposed to some other system"? In Figure 7 we will examine the situation. On the lower part of the graph I have plotted what is essentially a thermal. It shows the center of the thermal and goes out 3000 feet on either side. (This is air motion not what the variometer reads.) It shows about 170 feet per minute up in the middle and has some sink surrounding it. I will not argue about the model, all I am stating is that you've got a thermal and usually around thermals there is sink. I have balanced out the mass flow so this may not be a perfect model, but at least it illustrates what you fly through. We have two pilots for examples. Pilot #1 is the smartest guy that ever lived. I have plotted his airspeed as a function of his position in the thermal. He comes in from the left and starts to fly into sink. He speeds up and holds his speed through the heaviest sink, then zooms to get slowed up for the thermal, crosses the thermal and dives to get his speed way up to come out through the sink. Then gradually slows up until he is out on the other side. Now he's clever. He is able to anticipate what the thermal is doing ahead of him so he can arrange his speed to be exactly optimum -- that's hard to do. He's clever in that he can pull the G's that are required to perform this maneuver and still sense the thermal -- that's also very hard to do. Pilot #2 is kind of lazy. He pokes along at 75 knots just watching what is going on. When he gets in the vicinity of the thermal, gets the little bumps or whatever, he just pulls back a little bit and cruises through the thermal at about 65 knots. He finds out that it is really not strong enough to circle in and then leans it over a little bit and cruises on out through the sink at 75 knots. The question is: who did better and what were the prices paid? Well I took the two flight paths and went back through the previous curves -- integrated it all to get the average speeds flying through this 3,000 feet and what they would have to make up thermalling to get back to altitude. What the thermalling time would be to get back up to altitude. Well, the lazy guy poking around watching what he is doing achieved 37.9 miles per hour through the 3,000 feet. The real hotshot achieved 38.0.
So by flying true McCready speed the best you can do on a theoretical basis is about a quarter of a percent. But considering the thermalling time the lazy guy is going to require .96 minutes to get back to altitude and the hot shot is going to take 1.01 minutes to get back to altitude. If you assume that Pilot #1 is as smart as we said he is; which assumes he has prior knowledge of the thermal so he can arrange his speed, and pulling G's doesn't detract from his ability to know what the thermal is doing he still pays a 5% penalty for that leg of the course.
Based on this I have to conclude that the guy who is looking outside the cockpit and not worrying about his variometers and airspeed in the McCready sense is doing better. He's paying a quarter of a percent in speed but is saving 5% on his thermal requirements. I don't think that the average guy flying McCready speeds can do that good. I think he's always a little bit late. He's pretty darned fast when he zooms up into the thermal but he's late and so he's still going slow about the time he hits the sink, then he dives to get up speed. About the time he finds that he shouldn't be going so fast as he comes out. He's pretty inefficient, so I don't think he achieves the speed that is theoretically possible by a long ways. Yet, even if he did fly that profile, he would still pay a thermalling time penalty. These are my conclusions and are a philosophy to fly by. People should use McCready in moderation. The way to use McCready speeds if you have a McCready ring in your sailplane is to set it at zero. Set it for still air and use it to choose the speed between thermals unless you fly through some lift. There is little to be gained by speeding up beyond 75 knots in sink. The reason is that if you are in heavy sink you are also in a situation where you may have a problem coming up. You may not have too much altitude on the other side of the sink and so you must maximize your range. You maximize your range by flying at 75 knots and this also gives you time to think. That's worth doing in such a situation. There is little to be gained by hauling back on the stick to slow up for a thermal. You are pulling G's and can't feel the bumps. You are busy in the cockpit trying to manage your speed and not looking out to see what is going on. I think most people should just slow down a little bit and watch what is going on and if they don't like it, switch over and go back up to speed.
Question: Please survey the panel to see if they agree with this philosophy.
Answer: A.J. Smith: Although I agree with the philosophy, I would tend to deviate a little bit with the recommendation at the end. I would probably operate in a very narrow band of cruising speeds. I vary the cruising speed during the time of day according to the general thermal strengths we're having on that day, the thermal frequency, the sources of the thermal, the visual signs and all that sort of thing. I may be doing generally as Wil says, using 75 knots on pretty weak days. As the lift gets better and you get more streets, or more dependable clouds or whatever, I might push it on up another 10 knots, but not much more than that. As long as conditions remain fairly constant during the day, I keep the airspeed fairly constant between 75 and 85 knots. I don't do this sort of porpoising bit. I tend to slow down a little bit more than Wil suggests when there are a series of thermals in some pattern, but I certainly don't slow down very much with an individual thermal. I vary my operating airspeed a little bit towards the high side when the weather is really good.
George Moffat: I believe I do just about the same as A.J. Contrary to reputation I don't believe in flying very fast. Usually, I use one of two speeds about 75 or 85 knots, for general cruising purposes. It takes a fair amount of persuasion to vary much one way or the other. I have considerable reservations about porpoising unless you get Texas-type thermals that are very well-defined by clouds. These are predictable and usually quite large. In the east, I imagine as often as not, you'll lose more than you gain, by all this porpoising stuff. Wil, I have a question about one of your figures. Your charts were all based on the rising air mass of 430 feet per minute and a rate of sink of sailplane of around 130 feet per minute, but in climb attitude the rate of sink is probably more near 220 feet a minute in a standard class sailplane. That might move all your figures a little bit one way or another.
Question: Which way would it move them?
Answer: Slower.
Ben Greene: The glider (ASW-12) I'm flying now seems to me to be a little different. I don't exactly fly like that, which is why I am the low man on this totem pole, I guess. The one thing I have noticed is that with the inertia of the ASW-12 often times the 300 and 400 feet you zoom gives the real prize that puts you up higher where the thermal is better organized and probably stronger. This is perhaps an indirect gain from the zoom that might compensate for the G load loss. Ordinarily I generally fly a reduced McCready which gets back pretty close to what Wil is saying.
Dick Johnson: Well, I see we've got everybody committed to my technique. But I'm a little bit surprised that you admit it. As far as the zooms and the dives I have some very strong preferences about not flying with somebody that's doing that all the time because it makes me very nervous. I may have to armor-plate my floor board and canopy. Wil, I'd like to ask a question. Did you take into account the added flight path as you make a zoom and a climb and add that to the distance that the pilots had to go?
Wil Schuemann: That's not considered and is an additional loss. But surprisingly not as much as you would think. When I prepared the slides, I computed it. It's so small that it wasn't worth introducing the additional complexity.
Ben Greene: In zooming if you come in fairly low in a thermal strata, the thermal strength increases as you zoom and you gain that way. But if you are approaching the top where the thermal might have a tendency to weaken the zoom would be a negative thing. If you are zooming after you have made a glide you enter the thermal at a lower level. From this level up the thermal strength generally tends to increase. So you are zooming into an area of stronger lift whereas the guy who didn't zoom is down below, working weaker lift until he gets to the level you have zoomed to.
George Moffat: One more think about this zooming business. You really ought to practice it a lot if you really think it's going to pay. Because your timing has to be absolutely perfect. As Wil showed, all too often you're just nicely slowed up when you reach a 1,000 feet a minute sink on the far side of the thermal. That, somehow, doesn't improve your chances one bit.
Question: This presumes that you are flying through thermals and not intending to stop and circle?
Answer: George Moffat: Yes. You hardly ever know for sure what you intend to do until you come to the top of the zoom. I think I probably speak for the panel if I said that while we all do about what Wil suggests, we also keep in mind that there are quite a number of other factors such as the size and shape of the thermal, frequency of the thermals, the predictability of the next thermal. These are just a few of the various things you have to think about when you are flying.
Question: In coming down to a lower level [like a 1-26 Regatta] how would those speeds be applicable? 75 knots is close to the red line.
Answer: Wil Schuemann: This is a computed for a fiberglass ship without water. For a 1-26 these curves would be bunched up at the low speeds. Most 1-26 pilots know that you fly at 60 mph.
Question: Could you give us some idea of the effect of adding water to a standard class ship; 50 lbs. of water, 100 lbs. of water, 150 lbs. of water as far as effect on these speeds is concerned.
Answer: Wil Schuemann: Almost none. When you are flying with water, you can't afford to slow up as much, but you don't gain a lot by flying faster. You get the extra performance because of the added range between thermals.
Copyright Soaring Symposia All rights reserved. Permission to copy this article is granted for non-commercial use, in its entirety, and with this copyright notice attached.